In this section, solution methodologies including the multi-stage approach to dealing with stochastic supply and fuzzy programming to face fuzzy price and quality of vaccines are presented.
Multi-stage stochastic programming
The stochastic programming technique is widely used in various scopes such as finance, transportation, and energy optimization because of the prevalence of uncertainty in real-world decisions. It involves making optimal decisions based on available data at the time the decisions are made, without depending on future observations. The Two-Stage Stochastic Programming (TSSP) is a common approach, where the first-stage decisions are made at the beginning of the period, followed by the resolution of uncertainty, and the second-stage decisions are taken as corrective action at the end of the period. Stochastic programming is particularly useful for problems with a hierarchical framework, such as scheduling. The approach involves a combination of proactive and reactive decision-making to address uncertainty, where the second-stage variables respond reactively to the observed realization of uncertainty. The classical two-stage stochastic linear program with fixed recourse is a commonly used formulation for such problems. In summary, stochastic programming models, particularly MSSP, provide a powerful framework for decision-making under uncertainty, with applications in a wide range of industries and domains.
A stochastic programming model is a method used to optimize under uncertain conditions. It aims to find a solution that takes into account the uncertainty of problem parameters and optimizes goals selected by DMs. In general, an MSSP model with \(K\)-stages consists of several stochastic parameters named \({\upgamma }_{1}, {\upgamma }_{2} ,\dots , {\upgamma }_{\aleph -1}\), with each of them having realizations as scenarios. A scenario tree is used to integrate these separate scenarios, and the scenario probabilities are denoted as \({p}_{1}, {p}_{2} ,\dots , {p}_{s}\). A realization of stochastic parameters for scenario \(s\epsilon S\) is demonstrated by \(({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\)). In Fig. 2, a stochastic program with four stages \(\aleph =4\) and three periods \(t=3\) is typically represented as a sample of a scenario tree.
Figure 2
A sample of a scenario tree.
In an MSSP model, strategic decisions such as facility location and construction are made at the beginning and remain fixed in subsequent stages. Tactical decisions such as selection and allocation decisions must also be made before the realization of stochastic parameters, but they can be changed in each period. Operational decisions such as the flow between facilities are made when the stochastic parameters are realized at each stage. In summary, MSSP models involve making proactive–reactive decisions to address uncertainty, with the first-stage decisions being made based on available data, and the second-stage decisions being reactive to the observed realization of uncertainty.
In an MSSP model, the decision-making process should not be influenced by how stochastic parameters will be realized in the future. This means that the policy should not be anticipative, and non-anticaptivity constraints are imposed to formulate an MSSP model. By applying non-anticaptivity constraints, a public formulation for an MSSP including \(\aleph\)-stage can be introduced. To ensure that decisions are not influenced by future information, non-anticaptivity constraints must be incorporated into the optimization model of MSSP. These constraints guarantee that decision variables across different scenarios are equal, thereby preventing the anticipation of uncertain parameter values that are yet to be realized.
The decision vector for stages \(\aleph \epsilon \{\text{1,2},\dots ,\aleph \}\) and scenarios \(s\epsilon S\) is represented by \({x}^{\aleph s}\), with stochastic parameters being realized only after decisions are made at each stage. In the first stage of the scenario tree, the equation \({x}^{\aleph s}={x}^{\aleph {s}^{{{\prime}}}}\) applies to every pair of scenarios; \(s,{s}^{{{\prime}}}\epsilon S\). Additionally, for every stage \(\aleph >1\) and scenario \(s,{s}^{{{\prime}}}\epsilon S\) such that \(\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{{\prime}}}}, {\upgamma }_{2}^{{s}^{{{\prime}}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{{\prime}}}}\right)\), we have \({x}^{\aleph s}={x}^{\aleph {s}^{{\prime}}}\). The feasible range of DMs at stage \(\aleph\) and scenario \(s\) in the MSSP is determined by \({X}^{\aleph s}\) as follows:
$$Min \sum_{s=1}^{\left|S\right|}{p}_{s}\times f\left({x}^{1s},{x}^{2s},\dots ,{x}^{\aleph s},{\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)$$
(22)
$${x}^{\aleph s}\in {X}^{\aleph s}, \forall \aleph \in N , s\in S$$
(23)
$${x}^{\aleph s}={x}^{\aleph {s}^{{\prime}}}, \forall s, {s}^{\prime}\in S$$
(24)
$${x}^{\aleph s}={x}^{\aleph {s}^{{\prime}}}, \forall \aleph \in N, s, {s}^{\prime}\in S: \left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(25)
Developing a stochastic program based on scenarios presents a significant challenge in creating an efficient scenario tree after reducing the scenarios to represent stochastic parameters separately. Initially, the Monte Carlo simulation algorithm is utilized to generate a set of discrete scenarios for building a scenario tree. However, the large number of scenarios can render the problem unsolvable. This heuristic approach involves two methods for reducing backward and forward scenarios. In the backward algorithm, scenarios are eliminated one by one, while in the forward approach, scenarios are optimally selected one by one. Subsequently, the approach proposed by Heitsch and Romisch 54 is used to convert the scenario fan to a scenario tree, employing forward and backward algorithms for scenario reduction. Notably, a forward algorithm is used in each period to reduce the scenario and convert the scenario fan into a scenario tree. This process is essential for effectively managing the complexity of the scenario tree and ensuring that it accurately represents the stochastic parameters in the multistage stochastic program.
The non-anticipative constraints for the proposed model are as follows:
$${O}_{kts}={O}_{kt{s}{\prime}} \forall k\in K, t=1, (s,{s}{\prime})\in S$$
(26)
$${O}_{kts}={O}_{kt{s}{\prime}} \forall k\in K, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(27)
$${O}_{lts}{\prime}={O}_{lt{s}{\prime}}{\prime} \forall l\in L, t=1, (s,{s}{\prime})\in S$$
(28)
$${O}_{lts}{\prime}={O}_{lt{s}{\prime}}{\prime} \forall l\in L, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(29)
$${A}_{jts}={A}_{jt{s}{\prime}} \forall j\in J,t=1, (s,{s}{\prime})\in S$$
(30)
$${A}_{jts}={A}_{jts{\prime}} \forall j\in J, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{\prime}}, {\upgamma }_{2}^{{s}{\prime}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(31)
$${A{\prime}}_{its}={A{\prime}}_{its{\prime}} \forall i\in I, t=1,(s,{s}{\prime})\in S$$
(32)
$${A{\prime}}_{its}={A{\prime}}_{its{\prime}} \forall i\in I, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S: \left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(33)
$${A”}_{mts}={A”}_{mts{\prime}} \forall m\in M,t=1,(s,{s}{\prime})\in S$$
(34)
$${A”}_{mts}={A”}_{mts{\prime}} \forall m\in M, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S: \left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(35)
$${A{\prime}{\prime}{\prime}}_{ijts}={A{\prime}{\prime}{\prime}}_{ijts{\prime}} \forall i\in I, j\in J, t=1,(s,{s}{\prime})\in S$$
(36)
$${A{\prime}{\prime}{\prime}}_{ijts}={A{\prime}{\prime}{\prime}}_{ijts{\prime}} \forall i\in I, j\in J, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(37)
$${A””}_{jmts}={A””}_{jmts{\prime}} \forall j\in J,m\in M,t=1, (s,{s}{\prime})\in S$$
(38)
$${A””}_{jmts}={A””}_{jmts{\prime}} \forall j\in J,m\in M, t\in T/\left\{t=1\right\}, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(39)
The supplier selection (\(O , O{^{\prime}}\)) and allocation (\(A\), \(A{\prime}\), \(A”\), \(A{\prime}{\prime}{\prime}\), \(A””\)) decisions should be determined before the realization of uncertain inputs at each stage of the MSSP. Therefore, Constraints (26)–(39) illustrate the non-anticaptivity constraints of the MSSP.
$${y}_{kts}={y}_{kt{s}{\prime}}, \forall k\in K, t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(40)
$${y}_{lts}{\prime}={y}_{lt{s}{\prime}}{\prime} \forall l\in L,t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(41)
$${y”}_{lts}={y”}_{lt{s}{\prime}} \forall l\in L ,t\in T, \left(s,{s}^{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{\prime}}\right)$$
(42)
$${x}_{jts}={x}_{jts{\prime}} \forall j\in J ,t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(43)
$${x{\prime}}_{its}={x{\prime}}_{its{\prime}} \forall i\in I, t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(44)
$${x”}_{mrts}={x”}_{mrts{\prime}} \forall m\in M,r\in R, t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(45)
$${x{\prime}{\prime}{\prime}}_{ijts}={x{\prime}{\prime}{\prime}}_{ijts{\prime}} \forall i\in I,j\in J, t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(46)
$${x””}_{jmrts}={x””}_{jmrts{\prime}} \forall j\in J,m\in M, r\in R,t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(47)
$${u}_{mrts}={u}_{mrts{\prime}} \forall m\in M, r\in R, t\in T, \left(s,{s}{\prime}\right)\in S:\left({\upgamma }_{1}^{s}, {\upgamma }_{2}^{s}, \dots , {\upgamma }_{\aleph -1}^{s}\right)=\left({\upgamma }_{1}^{{s}^{{\prime}}}, {\upgamma }_{2}^{{s}^{{\prime}}}, \dots , {\upgamma }_{\aleph -1}^{{s}^{{\prime}}}\right)$$
(48)
In this study, the representation of uncertain parameters in period \(t\) under scenario \(s\) is denoted by \({\upgamma }_{\text{t}}^{s}\). The decision variables \({y}_{kts}, {y}_{lts}{\prime}, {y”}_{lts},{x}_{jts},{x{\prime}}_{its},{x”}_{mrts},{x{\prime}{\prime}{\prime}}_{ijts},{x””}_{jmrts}, and {u}_{mrts}\) are utilized. Equations (40) to (48) ensure that these variables adhere to non-anticipative constraints, preventing them from being influenced by future information.
Fuzzy mathematical programming
Fuzzy programming is a useful approach for addressing uncertainty in parameters and providing necessity in model mechanisms. Two main modules of fuzzy mathematical programming, possibility and necessity are proposed by Inuiguchi and Ramk 55 and Mula et al. 56, respectively. The possibility is utilized when an input parameter is uncertain or insufficient because of a lack of required data, involving the establishment of a distribution for each uncertain parameter according to the subjective opinions of DMs and objective data. Conversely, necessity can accommodate resistance to constraints, equations, and the adaptability of functions.
Possibility chance-constrained programming is a useful method in possibility programming that deals with probabilistic data in uncertain situations. This method allows the DM to set an optimum confidence level (\(\partial\)) to satisfy each possibility chance constraint, using possibility (\(POS\)) and necessity (\(NEC\)) as fuzzy measure standards to give confidence in models 57. The standards mentioned represent the most pessimistic and optimistic levels of the possibility of input occurrence. Equations (50)–(53) for \(\partial\) ≥0.5 are the crisp counterparts of the standards for a trapezoidal fuzzy variable. Additionally, Eq. (49) illustrates the corresponding membership function, where \(\widetilde{\mathcal{E}}=({\varepsilon }_{1},{\varepsilon }_{2}, {\varepsilon }_{3},{\varepsilon }_{4})\) with \({\varepsilon }_{1}<{\varepsilon }_{2}<{\varepsilon }_{3}<{\varepsilon }_{4}\). It is noteworthy that when \({\varepsilon }_{2}={\varepsilon }_{3}\), a triangular fuzzy variable is made from some changes in the trapezoidal one. Furthermore, based on Liu and Liu 58, Eqs. (54) and (55) show the expected value of the variable.
$${\mathbb{C}}_{\mathcal{x}}=\left\{\begin{array}{c}\frac{\mathcal{x}-{\varepsilon }_{1}}{{\varepsilon }_{2}-{\varepsilon }_{1}} if {\varepsilon }_{1}
(49)
$$\text{POS}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{\mathcal{x}-{\varepsilon }_{1}}{{\varepsilon }_{2}-{\varepsilon }_{1}}\ge \partial \leftrightarrow \mathcal{x}\ge \left(1-\partial \right){\varepsilon }_{1}+\partial {\varepsilon }_{2}$$
(50)
$$\text{POS}\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{{\varepsilon }_{4}-\mathcal{x}}{{\varepsilon }_{4}-{\varepsilon }_{3}}\ge \partial \leftrightarrow \mathcal{x}\le \partial {\varepsilon }_{3}+(1-\partial ){\varepsilon }_{4}$$
(51)
$$\text{NEC}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{\mathcal{x}-{\varepsilon }_{3}}{{\varepsilon }_{4}-{\varepsilon }_{3}}\ge \partial \leftrightarrow \mathcal{x}\ge \left(1-\partial \right){\varepsilon }_{3}+\partial {\varepsilon }_{4}$$
(52)
$$\text{N}EC \left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{{\varepsilon }_{2}-\mathcal{x}}{{\varepsilon }_{2}-{\varepsilon }_{1}}\ge \partial \leftrightarrow \mathcal{x}\le \partial {\varepsilon }_{1}+(1-\partial ){\varepsilon }_{2}$$
(53)
$${EV}_{\text{POS}}\left(\mathcal{E}\right)={\int }_{0}^{+\infty }\text{POS}\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\} dx-{\int }_{-\infty }^{0}\text{POS}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\} dx=\frac{{\varepsilon }_{3}+{\varepsilon }_{4}}{2}$$
(54)
$${EV}_{\text{NEC}}\left(\mathcal{E}\right)={\int }_{0}^{+\infty }\text{NEC}\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\} dx-{\int }_{-\infty }^{0}\text{NEC}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\} dx=\frac{{\varepsilon }_{1}+{\varepsilon }_{2}}{2}$$
(55)
In real-world conditions, DMs often exhibit fluctuating behavior between pessimistic and optimistic conditions. Equation (56) introduces a self-dual credibility (\(CRE\)) measure developed 58, which inspires a compromising attitude of DMs over both pessimistic and optimistic conditions. Furthermore, Eqs. (57)–(59) determine credibility criteria for confidence levels \(\partial\)≥0.5. Additionally, the expected value of the trapezoidal fuzzy variable for \({\varepsilon }_{1}\ge\) 0 is presented by Eq. (59).
$$\text{CRE}\left\{X\right\}=\frac{1}{2}(\text{POS}\left\{X\right\}+\text{NEC}\left\{X\right\})$$
(56)
$$\text{CRE}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{\mathcal{x}-{2\varepsilon }_{3}+{\varepsilon }_{4}}{{2(\varepsilon }_{4}-{\varepsilon }_{3})}\ge \partial \leftrightarrow \mathcal{x}\ge (2-2\partial ){\varepsilon }_{3}+(2\partial -1){\varepsilon }_{4}$$
(57)
$$\text{CRE}\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\}\ge \partial \leftrightarrow \frac{2{\varepsilon }_{2}-{\varepsilon }_{1}-\mathcal{x}}{2\left({\varepsilon }_{2}-{\varepsilon }_{1}\right)}\ge \partial \leftrightarrow \mathcal{x}\le \left(2\partial -1\right){\varepsilon }_{1}+(2-2\partial ){\varepsilon }_{2}$$
(58)
$${EV}_{\text{CRE }}\left(\mathcal{E}\right)={\int }_{0}^{+\infty }\text{CRE }\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\} d\mathcal{x}-{\int }_{-\infty }^{0}\text{CRE }\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\} d\mathcal{x}=\frac{{\varepsilon }_{1}+{\varepsilon }_{2}+{\varepsilon }_{3}+{\varepsilon }_{4}}{2}$$
(59)
The previous approach of using a midpoint to avoid extreme decisions may not be flexible enough for DMs. Xu and Zhou 59 proposed an alternative approach called the \(Me\) measure, which is a fuzzy number that is both flexible and avoids extreme decision-making. The approach described allows DMs to select a point from a spectrum of feasible alternatives based on real-life conditions using parameter settings in Eq. (60). In this method, \(\tau (0\le \tau \le 1)\) serves as a flexible criterion that enables DMs to make decisions reflecting real-life situations. For \(\tau\)=1, the maximum chance that the possibility (i.e., the most optimistic attitude) occurs, resulting in \(Me=POS\). Similarly, for \(\tau\)=0, the minimum chance that the possibility occurs, leading to \(Me=NEC\). For \(\tau\)=0.5, the \(\text{Me}=\text{CRE}\) C, which represents a compromising attitude of DMs. Equations (61), (62) demonstrate the \(Me\) measure, while Eq. (63) denotes the expected value of the trapezoidal fuzzy variable for \({\varepsilon }_{1}\ge 0\) based on the \(Me\) measure 59.
$$\text{Me}\left\{X\right\}=\tau \times \text{POS}\left\{X\right\}+\left(1-\tau \right)\times \text{NEC}\left\{X\right\}=\text{NEC}\left\{X\right\}+\tau \times (\text{POS}\left\{X\right\}+\text{NEC}\left\{X\right\})$$
(60)
$$\text{Me}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}=\left\{\begin{array}{c}0 if x\le {\varepsilon }_{1} \\ \tau \times \frac{\mathcal{x}-{\varepsilon }_{1}}{{\varepsilon }_{2}-{\varepsilon }_{1}} if {\varepsilon }_{1}\le x\le {\varepsilon }_{2}\\ \tau if {\varepsilon }_{2}\le x\le {\varepsilon }_{3}\\ \tau +\left(1-\tau \right)\times \frac{\mathcal{x}-{\varepsilon }_{3}}{{\varepsilon }_{4}-{\varepsilon }_{3}} if {\varepsilon }_{3}\le x\le {\varepsilon }_{4}\\ 1 if {\mathcal{x}\ge \varepsilon }_{4}\end{array}\right.$$
(61)
$$\text{Me}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}=\left\{\begin{array}{c}1 if x\le {\varepsilon }_{1} \\ \tau +\left(1-\tau \right)\times \frac{{\varepsilon }_{2}-\mathcal{x}}{{\varepsilon }_{2}-{\varepsilon }_{1}} if {\varepsilon }_{1}\le x\le {\varepsilon }_{2}\\ \tau if {\varepsilon }_{2}\le x\le {\varepsilon }_{3}\\ \tau \times \frac{{\varepsilon }_{4}-\mathcal{x}}{{\varepsilon }_{4}-{\varepsilon }_{3}} if {\varepsilon }_{3}\le x\le {\varepsilon }_{4}\\ 0 if {\mathcal{x}\ge \varepsilon }_{4}\end{array}\right.$$
(62)
$${EV}_{\text{Me}}\left(\mathcal{E}\right)={\int }_{0}^{+\infty }\text{Me}\left\{\widetilde{\mathcal{E}}\ge \mathcal{x}\right\} dx-{\int }_{-\infty }^{0}\text{Me}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\} dx=\left(1-\tau \right)\times (\frac{{\varepsilon }_{1}+{\varepsilon }_{2}}{2})+\tau \times (\frac{{\varepsilon }_{3}+{\varepsilon }_{4}}{2})$$
(63)
The \(Me\) measure, unlike previous mechanisms, does not equate \(Me\) \(\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\)≥ \(\partial\) and \(Me\) \(\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\)≥\(\partial\) for different confidence levels. Instead, it involves piecewise functions. DMs often use this approach in problems with high sensitivity to uncertain parameters to achieve possibility chance constraints while upholding an extremely reasonable chance. In sensitive scenarios such as health supply chain design, DMs often adopt a pessimistic approach. This implies that in these situations, they consider the pessimistic-optimistic parameter value to be less than 0.5. Representing the pessimistic method, the functions are akin to those depicted in Eqs. (64), (65).
$$\text{Me}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\ge \partial \leftrightarrow \tau +(1-\tau )\times \frac{\mathcal{x}-{\varepsilon }_{3}}{{\varepsilon }_{4}-{\varepsilon }_{3}}\ge \partial \leftrightarrow \mathcal{x}\ge \frac{\left(\partial -\tau \right){\varepsilon }_{4}+(1-\partial ){\varepsilon }_{3}}{1-\tau }$$
(64)
$$\text{Me}\left\{\widetilde{\mathcal{E}}\le \mathcal{x}\right\}\ge \partial \leftrightarrow \tau +(1-\tau )\times \frac{{\varepsilon }_{2}-\mathcal{x}}{{\varepsilon }_{2}-{\varepsilon }_{1}}\ge \partial \leftrightarrow \mathcal{x}\le \frac{\left(\partial -\tau \right){\varepsilon }_{1}+(1-\partial ){\varepsilon }_{2}}{1-\tau }$$
(65)
Blockchain technology consideration
In 2008, Nakamoto 60 introduced blockchain technology as a way to support transactions in the cryptocurrency Bitcoin. Blockchain is a decentralized, transparent, and secure platform where transactions between connected parties are recorded and stored on all participating computers, ensuring the data remains unchanged. While blockchain originated in the cryptocurrency field, it has since been explored and implemented across various industries. One notable example is the Smart Dubai 2021 project, which saw the integration of blockchain technology into government operations 61. SCM is one of the fields that has shown particular interest in blockchain technology. Researchers predict that blockchain will revolutionize supply chains by increasing the reliance on this innovative technology 62. Recent studies have explored the application of blockchain in diverse supply chain scenarios, such as the drug, food, healthcare, and research and development industries.
Platforms based on blockchains involve multiple components that work together. By combining them, blockchain renders contracted items to connected people (Fig. 3).
Figure 3
Smart contract operation.
Following the widespread COVID-19 outbreak and the success of various companies in vaccine production, the primary challenge for countries is to supply high-quality vaccines and plan for a seamless vaccination process. Some of the key challenges faced by countries in this context include:
I.
The limited supply and urgent global demand for vaccines in the COVID-19 epidemic have increased the likelihood of theft and fraud in the supply chain.
II.
Ensuring the quality of vaccines is a critical issue, particularly during the COVID-19 pandemic when the global demand for vaccines is high and the supply is limited. Quality control of purchased vaccines is an effective way to select suppliers and ensure that vaccines consistently meet appropriate levels of purity, potency, safety, and efficacy.
III.
In an epidemic situation, it is crucial to avoid congestion to ensure efficient and safe vaccine distribution. To achieve this, careful planning and prioritization of vaccinations are essential. Additionally, transparency and traceability of orders can help in careful planning and resource allocation.
IV.
Vaccines are perishable products that must be transported and saved under specific temperature conditions within the cold chain. The cold chain is a temperature-controlled system that includes all vaccine-related equipment and methods, ensuring that vaccines maintain their potency and effectiveness.
When evaluating the integration of blockchain technology across all components of the VSC network, as illustrated in Fig. 4, it is necessary to strike a tradeoff between cost and transparency. While blockchain offers enhanced security and transparency benefits, implementing it extensively can lead to a rise in installation costs. Therefore, a strategic approach is necessary to weigh the advantages of blockchain against the associated costs, ensuring a judicious trade-off between cost-effectiveness and the benefits of enhanced security and transparency. In the next subsection, we design a blockchain-enabled COVID-19 VSC network under epidemic conditions to consider the mentioned risks and transparency.
Figure 4
Blockchain platform for the COVID-19 VSC.
This research proposes a supply chain network for COVID-19 vaccines that uses blockchain and IoT. IoT is utilized for monitoring the storage conditions of vaccines, including factors such as temperature and humidity, to ensure their integrity during transportation and storage. By deploying IoT sensors on vaccine shipments and leveraging blockchain smart contracts, organizations can gain visibility into the COVID-19 VSC, confirm product arrival, and monitor the quality of vaccines during transportation and storage. These technologies can significantly enhance the efficiency, security, and transparency of the VSC network design.
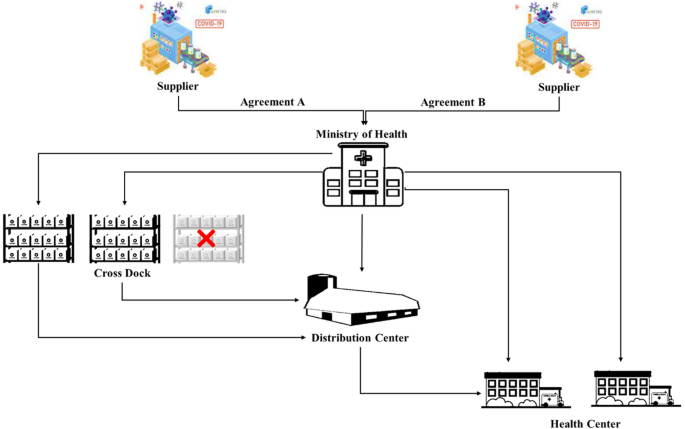
The aim is to merge the blockchain concept with the VSC to establish a blockchain-enabled multi-level VSC network. This supply chain configuration comprises five echelons: suppliers, MoH, CDCs, DCs, and HCs. Transparency serves as the key objective function in this setup. To facilitate this integration, CDCs and vehicles are equipped with IoT devices, enabling the conversion of the physical flow within the supply chain into a digital flow, thereby generating blocks. To create a blockchain, at least one member from the preceding level and one member from the next level must be linked to the equipped member. The blockchain concept is inherently decentralized, and the more blocks generated by the equipped CDCs, the greater the transparency achieved. The transparency criterion is based on the probability that an attacker will not succeed in manipulating the blockchain, as proposed by previous studies 63. The CDCs incur costs associated with being equipped with IoT tools to create the blockchain infrastructure and provide services to other levels. This cost is considered a proportion of the installation costs for that particular member. Members who join the blockchain will benefit from advantages such as transparency, tracking, better planning, and security. These benefits can lead to cost savings, and a portion of these savings can be factored in as revenue in the supply chain. Given that the members of the blockchain must negotiate the benefits, and these benefits are interactive between the members, they are treated as a factor of the cost of interactions between levels, such as transportation costs. The related notations and the integrated VSC and blockchain are as follows:
\(\mathcal{b}\in \mathcal{B}\):
Index of generated blocks in the VSC network
\({\mathcal{c}\mathcal{f}}_{i\mathcal{b}}^{p}\):
The assessment of the attacker’s advancement in terms of their lack of success, determined by the block type \(\mathcal{b}\) produced in CDC \(i\)
\({\mathcal{T}}_{i}^{A}\):
Blockchain technology adoption parameter in CDC \(i\) to create transparency in the VSC
\({\mathcal{t}}^{min},{\mathcal{t}}^{max}\):
Minimum and maximum values of transparency
\({\mathcal{c}\mathcal{r}}^{min}\):
Minimum number of CDCs participating in the blockchain
\(\partial\):
The ratio of the variable installation cost to the expense associated with utilizing blockchain technology
\({\ell}\):
The ratio of the variable transportation cost to the expense associated with utilizing blockchain technology
\({\mathcal{n}}_{i\mathcal{b}}\):
Equal to 1 If block type \(\mathcal{b}\) is installed in CDC \(i\), equal to 0
\({\mathcal{C}}_{i}\):
Equal to 1 If CDC \(i\) is equipped with an IoT tool, equal to 0
\({\mathcal{C}\mathcal{M}}_{i}^{1\to 2}\):
Equal to 1 if CDC \(i\) and the MoH participate to form the blockchain, equal to 0
\({\mathcal{C}\mathcal{D}}_{ij}^{2\to 3}\):
Equal to 1 if CDC \(i\) and the DC \(j\) participate to form the blockchain, equal to 0
\({x}_{its}^{{\prime}1\to 2}\):
Number of transported vaccines from the MoH to the CDC \(i\) at period \(t\) under scenario \(s;\)
\({x}_{ijts}^{{\prime}{\prime}{\prime}2\to 3}\):
Number of transported vaccines from the CDC \(i\) to the DC \(j\) at period \(t\) under scenario \(s;\)
$$\text{Max }\mathcal{T}\mathcal{r}=\sum_{i\in I,\mathcal{b}\in \mathcal{B}}{\mathcal{c}\mathcal{f}}_{i\mathcal{b}}^{p}\times {\mathcal{n}}_{i\mathcal{b}}$$
(66)
$$\text{Min F}=\sum_{i\in I}\partial \times {fc}_{i}\times {\mathcal{C}}_{i}-{\ell}\left(\sum_{i\in I}{tc{\prime}}_{i}\times {\mathcal{C}\mathcal{M}}_{i}^{1\to 2}+\sum_{i\in I,j\in J}{tc{\prime}{\prime}{\prime}}_{ij}\times {\mathcal{C}\mathcal{D}}_{ij}^{2\to 3}\right)+\sum_{i\in I}{fc}_{i}\times {Z}_{i}$$
$$+\sum_{s\in S}{p}_{s}\times \left(\sum_{k\in K}\sum_{t\in T}{fc}_{k}\times {O}_{kts}+\sum_{l\in L}\sum_{t\in T}{{fc}{\prime}}_{l}\times {O}_{lts}{\prime}+\sum_{k\in K}\sum_{t\in T}\widetilde{{pr}_{k}}\times {y}_{kts}+ \sum_{l\in L}\sum_{t\in T}\widetilde{{pr}_{l}{\prime}}\times {{y}{\prime}}_{lts}+\widetilde{{pr”}_{l}}\times {y”}_{lts}\right)$$
$$+\sum_{s\in S}{p}_{s}\times \left(\sum_{j\in J}\sum_{t\in T}{tc}_{j}\times {dis}_{j}\times {x}_{jts}+\sum_{i\in I}\sum_{t\in T}{tc{\prime}}_{i}\times {dis{\prime}}_{i}\times {x}_{its}^{{\prime}1\to 2}+\sum_{m\in M}\sum_{r\in R}\sum_{t\in T}{tc”}_{m}\times {dis”}_{m}\times {x”}_{mrts}+\sum_{i\in I}\sum_{j\in J}\sum_{t\in T}{tc{\prime}{\prime}{\prime}}_{ij}\times {dis{\prime}{\prime}{\prime}}_{ij}\times {x}_{ijts}^{{\prime}{\prime}{\prime}2\to 3}+\sum_{j\in J}\sum_{m\in M}\sum_{r\in R}\sum_{t\in T}{tc””}_{jm}\times {dis””}_{jm}\times {x””}_{jmrts}\right)+\sum_{m\in M}\sum_{r\in R}\sum_{t\in T}\sum_{s\in S}{p}_{s}\times \left({{sc}_{r}\times \omega }_{r}+{dc}_{m}{{\times \omega }{\prime}}_{m}\right)\times {u}_{mrts}$$
(67)
$${\mathcal{C}}_{i}\le {Z}_{i} \forall i\in I$$
(68)
$${\mathcal{C}}_{i}\le {\mathcal{C}\mathcal{M}}_{i}^{1\to 2} \forall i\in I$$
(69)
$${\mathcal{C}}_{i}\le \sum_{j}{\mathcal{C}\mathcal{D}}_{ij}^{2\to 3} \forall i\in I$$
(70)
$${\mathcal{C}\mathcal{M}}_{i}^{1\to 2}\le {x}_{its}^{{\prime}1\to 2} \forall i\in I,t\in T,s\in S$$
(71)
$${\mathcal{C}\mathcal{D}}_{ij}^{2\to 3}\le {x}_{ijts}^{{\prime}{\prime}{\prime}2\to 3} \forall i\in I,j\in J,t\in T,s\in S$$
(72)
$${\mathcal{C}\mathcal{M}}_{i}^{1\to 2}\le {\mathcal{C}}_{i} \forall i\in I$$
(73)
$${\mathcal{C}\mathcal{D}}_{ij}^{2\to 3}\le {\mathcal{C}}_{i} \forall i\in I,j\in J$$
(74)
$${\mathcal{t}}^{min}\le \sum_{i\in I}{\mathcal{T}}_{i}^{A}{\mathcal{C}}_{i}\le {\mathcal{t}}^{max}$$
(75)
$$\sum_{i\in I}{\mathcal{C}}_{i}\ge {\mathcal{c}\mathcal{r}}^{min}$$
(76)
$${\mathcal{C}}_{i}\ge \frac{\sum_{\mathcal{b}\in \mathcal{B}}{\mathcal{n}}_{i\mathcal{b}}}{\left|\mathcal{b}\right|} \forall i\in I$$
(77)
$$\sum_{i\in I}{\mathcal{n}}_{i\mathcal{b}}=1 \forall \mathcal{b}\in \mathcal{B}$$
(78)
$${x}_{its}^{{\prime}1\to 2},{x}_{ijts}^{{\prime}{\prime}{\prime}2\to 3},{\mathcal{C}\mathcal{M}}_{i}^{1\to 2},{\mathcal{C}\mathcal{D}}_{ij}^{2\to 3},{\mathcal{T}}_{i}^{A},{\mathcal{C}}_{i},{\mathcal{n}}_{i\mathcal{b}}\in \left\{\text{0,1}\right\}\forall i\in I,j\in j,\mathcal{b}\in \mathcal{B}$$
(79)
The primary goal of the initial Objective Function (66) is to maximize the overall number of extracted blocks in the equipped CDCs, fostering decentralization within the network. Conversely, in scenarios where an attacker seeks to tamper with blockchain data, their advancement in terms of failure, represented by the parameter \({\mathcal{c}\mathcal{f}}_{i\mathcal{b}}^{p}\) during attacks, is derived by aggregating the negative binomial distribution at each attack stage. As the quantity of blocks (\(\mathcal{b}\)) increases, the failure progression escalates due to the cumulative effect of additional distributions linked to the block count. Consequently, the attacker’s likelihood of success diminishes significantly with higher values of \(\mathcal{b}\) in the equipped CDCs. The second Objective Function (67) focuses on optimizing the financial aspects of the supply chain by minimizing operational costs.
Constraint (68) stipulates that block production is contingent upon the installation of CDC. Constraints (69) and (70) ensure that for CDC \(i\) to be part of the blockchain, there must be representation from both levels of the VSC. Constraints (71) and (72) elucidate that blockchain formation necessitates physical flow between different supply chain levels. Constraints (73) and (74) signify that equipping CDC \(i\) with an IoT tool is essential for block production within the blockchain. Constraint (75) sets the transparency thresholds expected from the supply chain manager. To promote decentralization, Constraint (76) guarantees a minimum number of independent CDCs within the blockchain. Constraints (77) and (78) define the total count of independent blocks generated in the CDCs. Constraint (79) outlines the binary decision variables.