theory
Scaled burial depth
High-energy chemical explosives produce high-temperature, high-pressure gases that exert strong radial compression on the surrounding sandy medium, forming a compression zone32. The TNT equivalent and the burial depth of the explosive have a significant influence on the type and size of the explosion crater33. To evaluate the destructive effects of different types of explosive sources under the same conditions, the concept of scaled burial depth is usually introduced, as shown in Equation 1, to evaluate the destructive effects of different types of explosive sources under consistent conditions. The impact of explosion damage over multiple explosions is evaluated34. (1):
$$z=\frac{d}{{{{({W_{TNT}})}^{1/3}}}}$$
(1)
where z is the scaled burial depth, d is the burial depth, and WTNT is the TNT equivalent of the explosive.
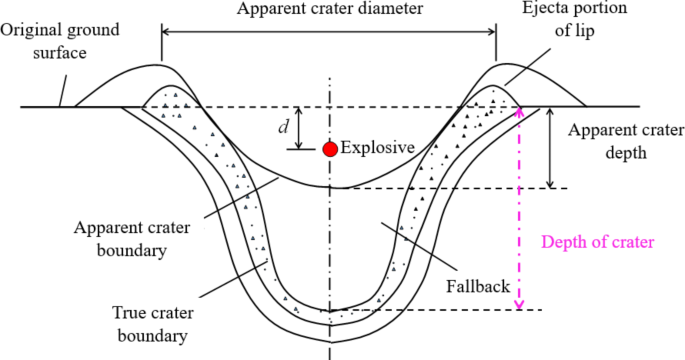
The burial depth of the explosive determines the type and size of the explosion crater35. When the gunpowder is buried at a shallow depth, the sand around the gunpowder is rapidly crushed by the detonation gas generated after the explosion, and the sand around the gunpowder gains an initial upward velocity due to the compression and exfoliation effects of the explosion, resulting in the throwing phenomenon. It happens. As the burial depth of the explosive increases, the suppressing effect of the sand covering the explosive on the drop of the explosion gradually increases. As shown in Figure 237, the explosion gases only cause a small cavity to form in the local sand around the explosive, which collapses under the weight of the sand above, eventually forming a collapsed crater. I will. Due to the increase, the energy generated by the explosion only causes vibrations in the foundation, there is no obvious change in the surface, and a camouflage is formed38.
Figure 1 Figure 2 2
Collapsed crater.
aspect ratio
Based on scaling laws, the linear dimension L of the explosion crater can be expressed as a constant multiplied by the equivalent TNT Wα of the explosive. Here, α is a coefficient that depends on whether gravity is ignored39. Baker et al. published a dimensional study using six parameters to model cratering phenomena in underground explosions10. Obtain the aspect ratio (rc) function as shown in Equation 1. (2) After much analysis and observation.
$${r_c}=\frac{R}{d}=f\left( {\frac{{{W^{\frac{7}{{24}}}}}}{{{\sigma ^{\ frac{1}{6}}}{K^{\frac{1}{8}}}d}}} \right)$$
(2)
where W is the explosive equivalent TNT. d is the depth of the explosive. R is the radius of the crater. \(\sigma\) is the stress dimension and is related to the strength of the sand. K is the force divided by body length.
As shown in equation (2), the specific gravity \(\rho g\) is measured for K, and \(\rho {c^2}\) is measured for \(\sigma\). where c is the detonation velocity in the sand. This empirical formula for the difference in sand density can be written as \({r_c}\) and \(\frac{{{W^{\frac{7}{{24}}}}}}{{{\rho ^{\ frac{7}{{24}}}}{c^{\frac{1}{3}}}{\rho ^{\frac{1}{8}}}d}}\) Graph, the result is small It can be clearly explained that there is a change.
field test
calcareous sand
The sand used in the field tests is calcareous sand from the South China Sea, which is formed by corals in the ocean through long-term geological and weathering processes40. Figure 3 shows a physical photograph and an electron microscope scanning photograph of the calcareous sand. As shown in Figure 3, calcareous sand particles have unique physical properties such as irregular shapes and high porosity. The particle size distribution curve of calcareous sand is shown in Figure 4. The mechanical parameters of calcareous sand obtained according to the Chinese geotechnical test method standard are shown in Table 1.
Figure 3Figure 3 4
Particle size distribution curve.
Table 1 Calcareous sand parameters. Field test design
A large TNT-equivalent explosion in sand would release enormous amounts of energy, requiring higher standards of test equipment and stricter safety measures, which would necessarily increase both the cost and duration of the test. 41. In many cases, a small TNT equivalent explosion in sand is preferred for testing42. In the field test, a factory-customized black powder with an equivalent weight of 5 g of TNT was used, as shown in Figure 5. In the field test, the explosive was buried at the depth of the test design and connected to a fuse. As shown in Figure 6, a 4 mm diameter plastic pipe is wrapped around the fuse to increase the probability of successful field testing and to prevent foundation water from wetting the fuse.
Figure 5 Figure 5 6
By changing the burial depth of the gunpowder, different scales of burial depth conditions were established. The range of burial depth for installing explosives is set at 0.03 to 0.37 m, respectively, as shown in Table 2. Considering the discrete nature of field tests, we set up three sets of parallel tests with the same burial depth conditions.
Table 2 Field test design conditions.
numerical simulation
SPH-FEM combination algorithm
Smooth particle hydrodynamics is a meshless Lagrangian computational method43. Its adaptability allows it to better handle large deformation problems and handle material interfaces smoothly and continuously44. The SPH method discretizes the problem domain through a set of particles, where each particle can convey field variables such as density, velocity, stress, and displacement45. The SPH method uses an integral formula to approximate a particular field function and discretize it into a series addition problem as shown in Equation 1. (3). Equation (3) is a general SPH approximation equation, and its schematic diagram is shown in Figure 7. As shown in Fig. 7, h is the support domain radius of the kernel function. This equation can be used to estimate any field variable in continuous space.
$$f({r_i})=\int\limits_{\Omega } {f(r)} {W_{ij}}dr \about \sum\limits_{j} {{V_j}{f_j}} {W_{ ij}}$$
(3)
Here \({W_{ij}}\) is a kernel function, i.e. a dimensionless function. \(\Omega\) is the support domain for kernel functions. i is the particle to be investigated. j is a particle near i. r is the distance between particles. \({V_b}\) is the volume of particle j.
A complete SPH particle model significantly increases computation time and may also introduce issues such as boundary restriction problems46. Therefore, the modeling process typically establishes SPH particles for the explosive and the surrounding sand, and uses finite elements away from the explosive. As shown in Figure 8, the keyword *CONGTROL_TIED_NODE_TO_SURFACE_OFFSET was used to constrain the mutual fixed coupling between the SPH particles and the finite elements. Set the SPH particle as the slave surface, set the finite element as the master surface, and constrain the slave node. It enables the transfer of particle velocity, stress, mass, and other information to finite elements.
Figure 7
Schematic diagram of kernel functionality.
Figure 8
SPH-FEM coupling algorithm.
numerical model
To accurately analyze the characteristics of the explosion crater, a 3D finite element model was established based on a 1:1 similarity ratio. The overall size of the numerical model is 0.9 m*0.9 m*0.4 m, of which the range of the SPH part is 0.6 m*0.6 m*0.3 m. The dimensions of one quarter of the numerical model are shown in Figure 9. The size of the elements plays a decisive role in calculation accuracy and resource consumption. The trade-off between accuracy and computational resources is one of the important problems to be solved in numerical analysis. After repeated calculations, the size of the elements in the model was set to 1 cm. The numerical model consists of 223,240 finite elements and 123,068 SPH particles, including 47 SPH particles representing explosives. By changing the position of the explosive SPH particles, different burial depths of the explosive in the numerical model are controlled. To simulate the field tests as realistically as possible, the top surface of the numerical model is set as a free-form surface, normal constraints are applied to the sides of the model, and full constraints are applied to the bottom surface.
Figure 9
Quarterly 3D SPH-FEM model.
calcareous sand model
The key to the numerical simulation of the sand explosion problem lies in the rational selection of the sand model and parameters47. By evaluating constitutive models suitable to describe sand in the LS-DYNA software, the *MAT_005_ SOIL_AND_FOAM model, one of the earliest constitutive models to support the SPH algorithm, was selected48. This model is simple and the material parameters can be easily obtained, so it is widely used to address the problem of explosion in calcareous sand foundations.
The stress-strain curves of the model during loading and unloading are shown in Figure 10. Ten sets of data are used to perform a multi-segment linear approximation of the compression equation. The equation of state parameters recommended by Wu et al.49 and suitable for calcareous sand in calculations are shown in Table 3. The density of calcareous sand is 1370 kg/m3, the shear modulus is 106.3 MPa, the bulk modulus is 587.3 MPa, and the shear yield coefficients in the shear plane are a0 = 73.85 kPa2, a1 = 13.19 kPa, and a2 = 0.3.
Figure 10
Schematic diagram of the pressure and volume response of sand.
Table 3 Parameters of equation of state for calcareous sand. explosion model
The explosives are simulated using the high-energy explosives model and JWL equations in LS-DYNA software 37 . The JWL equation for explosives can accurately describe the pressure, volume, and energy characteristics of the explosion during the explosion process, as shown in Equation 1. (4):
$${P_e}=A(1 – \frac{\omega }{{{R_1}{V_r}}}){e^{ – {R_1}{V_r}}}+B(1 – \frac{\omega }{{{R_2}{V_r}}}){e^{ – {R_2}{V_r}}}+\frac{{\omega {E_0}}}{{{V_r}}}$$
(4)
Here, A, B, \({R_1}\), \({R_2}\), \(\omega\) are the explosion parameters. \({P_e}\) is the pressure created by the explosion. \({V_r}\) is the relative specific volume. \({E_0}\) is the specific internal energy of the explosion product.
The parameters of the explosives used in the paper are shown in Table 450.
Table 4 Material parameters of explosives model.
Source link